Given a binary tree root, a node X in the tree is named good if in the path from root to X there are no nodes with a value greater than X.
Return the number of good nodes in the binary tree.
Example 1:
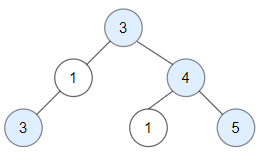
Input: root = [3,1,4,3,null,1,5]
Output: 4
Explanation: Nodes in blue are good.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.
Example 2:
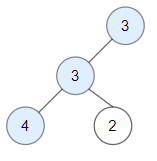
Input: root = [3,3,null,4,2]
Output: 3
Explanation: Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.
Example 3:
Input: root = [1]
Output: 1
Explanation: Root is considered as good.
1) Explain the problem
We need to count the number of "good" nodes in a binary tree. A node X in the binary tree is considered "good" if the path from the root to X does not contain any node with a value greater than X.
2) Short easy to remember solution/approach
Use depth-first search (DFS) to traverse the tree while keeping track of the maximum value encountered on the path from the root to the current node. Count the node as "good" if its value is greater than or equal to this maximum value.
3) Solution in Javascript with code commenting
class TreeNode {
constructor(val, left = null, right = null) {
this.val = val;
this.left = left;
this.right = right;
}
}
function countGoodNodes(root) {
function dfs(node, maxSoFar) {
if (!node) return 0;
// A node is "good" if its value is greater than or equal to the maximum value encountered so far
let good = node.val >= maxSoFar ? 1 : 0;
// Update the maximum value encountered so far
maxSoFar = Math.max(maxSoFar, node.val);
// Recursively count good nodes in the left and right subtrees
good += dfs(node.left, maxSoFar);
good += dfs(node.right, maxSoFar);
return good;
}
return dfs(root, root.val);
}
// Example usage:
let root = new TreeNode(3);
root.left = new TreeNode(1);
root.right = new TreeNode(4);
root.left.left = new TreeNode(3);
root.right.left = new TreeNode(1);
root.right.right = new TreeNode(5);
console.log(countGoodNodes(root)); // Output: 4
4) Explanation of the solution in an easy-to-understand way. Explain it like a 10-year-old.
Imagine you are walking from the bottom of a hill (the root) to the top (each node). You have a rule that you can only count the spots (nodes) where the height (value) is greater than or equal to the highest spot you've seen so far on your path. You keep walking, updating the highest spot you've seen, and count how many good spots you find.
5) Code explanation in pointers
Define a
TreeNodeclass to represent each node in the tree.Create a
countGoodNodesfunction that:Defines a helper function
dfsto:Return 0 if the node is
null.Check if the node's value is greater than or equal to the maximum value encountered so far and count it as "good" if true.
Update the maximum value encountered so far.
Recursively count good nodes in the left and right subtrees.
Return the total count of good nodes.
Start the DFS traversal from the root with its value as the initial maximum value.
Use the
countGoodNodesfunction to count the good nodes in the tree.
6) Complexities
Time Complexity: (O(n)) - Each node is visited once.
Space Complexity: (O(h)) - Where (h) is the height of the tree. This is due to the recursion stack.
