LietCode
Balanced Binary Tree (Easy)

Balanced Binary Tree (Easy)

Abhi's photo
Abhi
·

3 min read

Given a binary tree, determine if it is height-balanced.

Example 1:

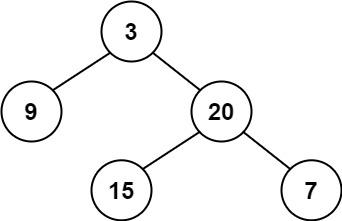
Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

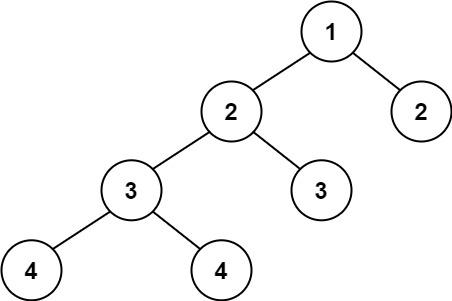
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true

1) Explain the problem

We need to check if a given binary tree is height-balanced. A binary tree is height-balanced if for every node in the tree, the depth of the left and right subtrees differs by no more than 1.

2) Short easy to remember solution/approach

Use a depth-first search (DFS) approach to calculate the height of each subtree and check the balance condition at each node. Return false immediately if any subtree is not balanced.

3) Solution in Javascript with code commenting

class TreeNode {
    constructor(val, left = null, right = null) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

function isBalanced(root) {
    // Helper function to determine the height and check if balanced
    function checkHeight(node) {
        if (node === null) return 0;

        // Recursively check the height of left subtree
        let leftHeight = checkHeight(node.left);
        if (leftHeight === -1) return -1; // Not balanced

        // Recursively check the height of right subtree
        let rightHeight = checkHeight(node.right);
        if (rightHeight === -1) return -1; // Not balanced

        // If the current node is not balanced
        if (Math.abs(leftHeight - rightHeight) > 1) return -1;

        // Return the height of the current node
        return Math.max(leftHeight, rightHeight) + 1;
    }

    // Start the check from the root
    return checkHeight(root) !== -1;
}

// Example usage:
let tree = new TreeNode(1);
tree.left = new TreeNode(2);
tree.right = new TreeNode(3);
tree.left.left = new TreeNode(4);
tree.left.right = new TreeNode(5);
tree.left.left.left = new TreeNode(6);

console.log(isBalanced(tree)); // Output: false (not balanced)

4) Explanation of the solution in an easy-to-understand way. Explain it like a 10-year-old.

Imagine you have a seesaw (a tree) and you want to check if it is balanced. You start from one end (the root) and check the balance at every point (node). If at any point, one side of the seesaw is much heavier (one subtree is much deeper) than the other side, it’s not balanced. You keep checking each point until you reach the end or find it unbalanced.

5) Code explanation in pointers

  • Define a TreeNode class to represent each node in the tree.

  • Create an isBalanced function that:

    • Defines a helper function checkHeight to:

      • Return 0 if the node is null.

      • Recursively calculate the height of the left and right subtrees.

      • Return -1 if either subtree is not balanced.

      • Check if the current node is balanced by comparing the heights of the left and right subtrees.

      • Return the height of the current node.

    • Start checking from the root.

    • Return true if the tree is balanced and false otherwise.

6) Complexities

  • Time Complexity: (O(n)) - Each node is visited once.

  • Space Complexity: (O(h)) - Where (h) is the height of the tree. This is due to the recursion stack.

Tree