LietCode
Diameter of Binary Tree (Easy)

Diameter of Binary Tree (Easy)

Abhi's photo
Abhi
·

3 min read

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

Example 1:

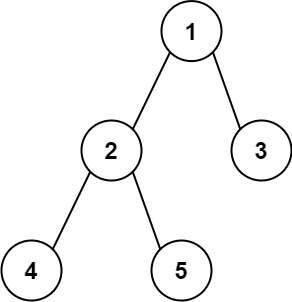
Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Example 2:

Input: root = [1,2]
Output: 1

1) Explain the problem

We need to find the diameter of a binary tree. The diameter is defined as the length of the longest path between any two nodes in the tree. This path may or may not pass through the root. The length of the path is measured by the number of edges between the nodes.

2) Short easy to remember solution/approach

Use depth-first search (DFS) to calculate the height of each subtree and simultaneously keep track of the longest path found. The diameter will be the maximum value of these paths.

3) Solution in Javascript with code commenting

class TreeNode {
    constructor(val, left = null, right = null) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

function diameterOfBinaryTree(root) {
    let diameter = 0;

    // Helper function to calculate the height of a tree
    function height(node) {
        if (node === null) return 0;

        // Recursively get the height of the left and right subtrees
        let leftHeight = height(node.left);
        let rightHeight = height(node.right);

        // Update the diameter if the path through the current node is larger
        diameter = Math.max(diameter, leftHeight + rightHeight);

        // Return the height of the current node
        return Math.max(leftHeight, rightHeight) + 1;
    }

    height(root);
    return diameter;
}

// Example usage:
let tree = new TreeNode(1);
tree.left = new TreeNode(2);
tree.right = new TreeNode(3);
tree.left.left = new TreeNode(4);
tree.left.right = new TreeNode(5);

console.log(diameterOfBinaryTree(tree)); // Output: 3

4) Explanation of the solution in an easy-to-understand way. Explain it like a 10-year-old.

Imagine you have a big tree in your backyard, and you want to find the longest path you can walk starting from one branch, going through the tree, and ending at another branch. To figure this out, you check how tall each part of the tree is (like measuring each branch) and then see which path gives you the longest walk. You keep track of the longest path you find while you measure.

5) Code explanation in pointers

  • Define a TreeNode class to represent each node in the tree.

  • Create a diameterOfBinaryTree function that initializes the diameter to 0.

  • Define a helper function height that:

    • Returns 0 if the node is null.

    • Recursively calculates the height of the left and right subtrees.

    • Updates the diameter with the sum of the heights of the left and right subtrees.

    • Returns the height of the current node.

  • Call the height function starting from the root.

  • Return the diameter.

6) Complexities

  • Time Complexity: (O(n)) - Each node is visited once.

  • Space Complexity: (O(h)) - Where (h) is the height of the tree. This is due to the recursion stack.

Tree