LietCode
Lowest Common Ancestor of a Binary Search Tree (Medium)

Lowest Common Ancestor of a Binary Search Tree (Medium)

Abhi's photo
Abhi
·

5 min read

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

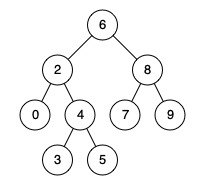
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [2,1], p = 2, q = 1
Output: 2

1) Explain the problem

We need to find the lowest common ancestor (LCA) of two given nodes in a binary search tree (BST). The LCA is defined as the lowest node in the tree that has both given nodes as descendants (a node can be a descendant of itself).

2) Short easy to remember solution/approach

Leverage the properties of a BST to find the LCA. If both nodes are smaller than the current node, the LCA is in the left subtree. If both nodes are larger, the LCA is in the right subtree. Otherwise, the current node is the LCA.

3) Solution in Javascript with code commenting

class TreeNode {
    constructor(val, left = null, right = null) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

function lowestCommonAncestor(root, p, q) {
    // Base case
    if (!root) return null;

    // If both p and q are smaller than root, LCA lies in left subtree
    if (p.val < root.val && q.val < root.val) {
        return lowestCommonAncestor(root.left, p, q);
    }

    // If both p and q are larger than root, LCA lies in right subtree
    if (p.val > root.val && q.val > root.val) {
        return lowestCommonAncestor(root.right, p, q);
    }

    // If p and q are on different sides or one is the root, root is the LCA
    return root;
}

// Example usage:
let root = new TreeNode(6);
root.left = new TreeNode(2);
root.right = new TreeNode(8);
root.left.left = new TreeNode(0);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(7);
root.right.right = new TreeNode(9);
root.left.right.left = new TreeNode(3);
root.left.right.right = new TreeNode(5);

let p = root.left; // Node with value 2
let q = root.left.right; // Node with value 4

console.log(lowestCommonAncestor(root, p, q)); // Output: Node with value 2

4) Explanation of the solution in an easy-to-understand way. Explain it like a 10-year-old.

Imagine you are on a tree and looking for the common parent branch where two branches split off. If you are higher up and see that both branches you are looking for are on one side, you move down that side. If they are on different sides or one is directly below you, then you are at the spot where the branches split off, which means you found the common parent.

5) Code explanation in pointers

  • Define a TreeNode class to represent each node in the tree.

  • Create a lowestCommonAncestor function that:

    • Returns null if the root is null.

    • Recursively checks the left subtree if both nodes are smaller than the root.

    • Recursively checks the right subtree if both nodes are larger than the root.

    • Returns the root if the nodes are on different sides or one node is the root.

  • Use the lowestCommonAncestor function to find the LCA of two given nodes.

Explanation of how the solution worked

Let's break down how the solution to finding the lowest common ancestor (LCA) in a binary search tree (BST) works step by step.

1. Understanding the Binary Search Tree (BST) Properties

A BST has the following properties:

  • The left child of a node contains a value less than the node's value.

  • The right child of a node contains a value greater than the node's value.

Using these properties, we can efficiently determine the LCA of two nodes.

2. Steps of the Solution

  1. Check the Base Case:

    • If the root is null, return null. This means we have reached the end of a path without finding the LCA.

  2. Compare Node Values with Root:

    • If both p and q have values less than the root's value, the LCA must be in the left subtree. Thus, we recursively search the left subtree.

    • If both p and q have values greater than the root's value, the LCA must be in the right subtree. Thus, we recursively search the right subtree.

    • If p and q are on different sides of the root or one of them is the root, then the root itself is the LCA.

3. Example Walkthrough

Let's walk through an example with the following BST:

        6
       / \
      2   8
     / \ / \
    0  4 7  9
      / \
     3   5

Given nodes p with value 2 and q with value 4, let's find their LCA.

  • Start at the root (node 6):

    • Both p.val (2) and q.val (4) are less than 6, so move to the left subtree (node 2).

  • At node 2:

    • p.val (2) equals 2, and q.val (4) is greater than 2. Since one node is equal to the current node and the other is on the other side, this node (2) is the LCA.

4. Key Points:

  • The solution leverages the BST property that all values in the left subtree are less than the root and all values in the right subtree are greater than the root.

  • By recursively checking the left or right subtree based on the values of p and q, we efficiently narrow down the LCA.

  • When p and q are on different sides of a node, or one is the root, that node is the LCA.

This solution works efficiently because it avoids unnecessary comparisons and leverages the sorted nature of BSTs.

6) Complexities

  • Time Complexity: (O(h)) - Where (h) is the height of the tree. In the worst case, we may need to traverse from the root to the deepest leaf.

  • Space Complexity: (O(h)) - Due to the recursion stack.

TreeTrees