LietCode
N-Queens II

N-Queens II

Abhi's photo
Abhi
·

3 min read

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Example 1:

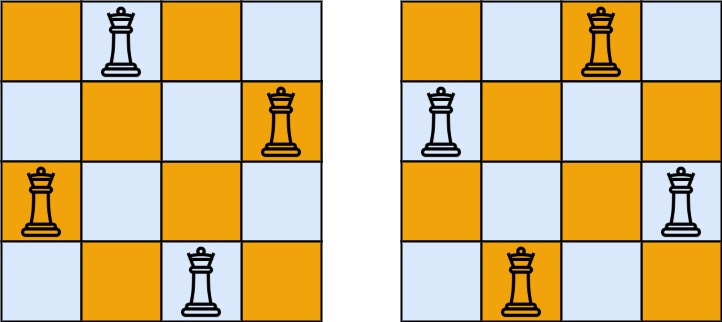
Input: n = 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown.

Example 2:

Input: n = 1
Output: 1

1) Explain the problem

The N-Queens problem involves placing n queens on an n x n chessboard such that no two queens threaten each other. This means no two queens can be in the same row, column, or diagonal. The "N-Queens II" problem requires you to count all distinct solutions to this problem.

2) Short easy to remember solution/approach

  1. Use backtracking to place queens on the board.

  2. Use sets to keep track of columns and diagonals that are already occupied by queens.

  3. Count valid configurations.

3) Solution in JavaScript with code commenting

function totalNQueens(n) {
    let count = 0;
    const cols = new Set();
    const diag1 = new Set(); // Left diagonal
    const diag2 = new Set(); // Right diagonal

    function backtrack(row) {
        if (row === n) {
            count++;
            return;
        }

        for (let col = 0; col < n; col++) {
            if (cols.has(col) || diag1.has(row - col) || diag2.has(row + col)) {
                continue;
            }

            cols.add(col);
            diag1.add(row - col);
            diag2.add(row + col);

            backtrack(row + 1);

            cols.delete(col);
            diag1.delete(row - col);
            diag2.delete(row + col);
        }
    }

    backtrack(0);
    return count;
}

// Example usage:
const n = 4;
console.log(totalNQueens(n)); // Output: 2

4) Explanation the solution in an easy-to-understand way with real-life example

Imagine you have a n x n chessboard and you want to place n queens on it in such a way that no two queens can attack each other. A queen can attack any piece in the same row, column, or diagonal. You need to find out how many different ways you can place these queens.

For example, with a 4x4 board (n=4), you need to figure out all the unique ways to place 4 queens where none of them can attack each other.

5) Code explanation in pointers

  • Initialize variables: count to keep track of valid configurations, and three sets to keep track of occupied columns and diagonals.

  • Backtracking function: This function tries to place queens row by row.

  • Base case: If all rows are filled, increment the count of valid solutions.

  • Loop through columns: For each row, try placing a queen in each column.

  • Check for conflicts: Skip columns and diagonals that are already occupied by another queen.

  • Place queen: Add the column and diagonals to the sets to mark them as occupied.

  • Recursive call: Move to the next row.

  • Backtrack: Remove the queen and free up the column and diagonals for other configurations.

  • Return result: After exploring all possibilities, return the count of valid solutions.

6) Complexities

  • Time complexity: (O(n!)) because there are (n) choices for the first row, (n-1) choices for the second row, and so on.

  • Space complexity: (O(n)) for the recursion stack and the sets used to track columns and diagonals.

backtracking