You are given the root of a binary tree containing digits from 0 to 9 only.
Each root-to-leaf path in the tree represents a number.
- For example, the root-to-leaf path
1 -> 2 -> 3represents the number123.
Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.
A leaf node is a node with no children.
Example 1:
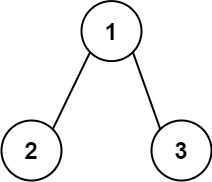
Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.
Example 2:
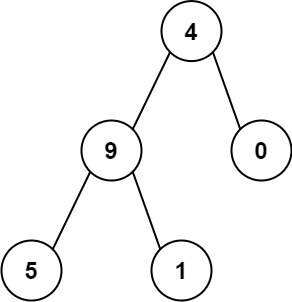
Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.
1) Explain the problem
We need to calculate the sum of all numbers formed by root-to-leaf paths in a binary tree. Each path from the root to a leaf represents a number formed by concatenating the node values along the path.
2) Short easy to remember solution/approach
Use depth-first search (DFS) to traverse the tree. Keep track of the current number formed by the path from the root to the current node. When a leaf node is reached, add the current number to the total sum.
3) Solution in Javascript with code commenting
class TreeNode {
constructor(val, left = null, right = null) {
this.val = val;
this.left = left;
this.right = right;
}
}
function sumNumbers(root) {
function dfs(node, currentNumber) {
if (!node) return 0;
// Update the current number
currentNumber = currentNumber * 10 + node.val;
// If the node is a leaf, return the current number
if (!node.left && !node.right) {
return currentNumber;
}
// Recursively calculate the sum for the left and right subtrees
let leftSum = dfs(node.left, currentNumber);
let rightSum = dfs(node.right, currentNumber);
// Return the total sum
return leftSum + rightSum;
}
// Start the DFS with the root and initial number 0
return dfs(root, 0);
}
// Example usage:
let root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
console.log(sumNumbers(root)); // Output: 25 (12 + 13)
root = new TreeNode(4);
root.left = new TreeNode(9);
root.right = new TreeNode(0);
root.left.left = new TreeNode(5);
root.left.right = new TreeNode(1);
console.log(sumNumbers(root)); // Output: 1026 (495 + 491 + 40)
4) Explanation of the solution in an easy-to-understand way. Explain it like a 10-year-old.
Imagine you have a tree, and each branch has numbers on it. You start at the root and move to the leaves, collecting numbers along the way to form a big number. When you reach a leaf, you add the big number to your total sum. You do this for all branches and then add up all the big numbers you collected.
5) Code explanation in pointers
Define a
TreeNodeclass to represent each node in the tree.Create a
sumNumbersfunction that:Defines a helper function
dfsto:Return 0 if the node is
null(base case).Update the current number by appending the node's value.
Return the current number if the node is a leaf.
Recursively calculate the sum for the left and right subtrees.
Return the total sum of the left and right subtrees.
Start the DFS with the root and initial number 0.
Use the
sumNumbersfunction to calculate the total sum of all root-to-leaf numbers.
Note : When traversing a binary tree to form numbers from root to leaf, we need to concatenate the node values as digits to form a single number. For example, if we move from the root node with value 1 to a child node with value 2, the number formed should be 12.
6) Complexities
Time Complexity: (O(n)) - Each node is visited once.
Space Complexity: (O(h)) - Where (h) is the height of the tree. This is due to the recursion stack.
