LietCode
Sum Root to Leaf Numbers (Medium)

Sum Root to Leaf Numbers (Medium)

Abhi's photo
Abhi
·

4 min read

You are given the root of a binary tree containing digits from 0 to 9 only.

Each root-to-leaf path in the tree represents a number.

  • For example, the root-to-leaf path 1 -> 2 -> 3 represents the number 123.

Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.

A leaf node is a node with no children.

Example 1:

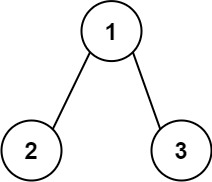
Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

Example 2:

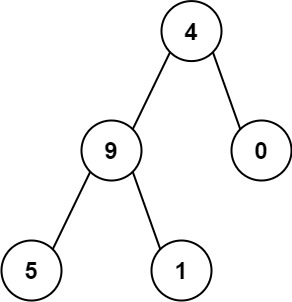
Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

1) Explain the problem

We need to calculate the sum of all numbers formed by root-to-leaf paths in a binary tree. Each path from the root to a leaf represents a number formed by concatenating the node values along the path.

2) Short easy to remember solution/approach

Use depth-first search (DFS) to traverse the tree. Keep track of the current number formed by the path from the root to the current node. When a leaf node is reached, add the current number to the total sum.

3) Solution in Javascript with code commenting

class TreeNode {
    constructor(val, left = null, right = null) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

function sumNumbers(root) {
    function dfs(node, currentNumber) {
        if (!node) return 0;

        // Update the current number
        currentNumber = currentNumber * 10 + node.val;

        // If the node is a leaf, return the current number
        if (!node.left && !node.right) {
            return currentNumber;
        }

        // Recursively calculate the sum for the left and right subtrees
        let leftSum = dfs(node.left, currentNumber);
        let rightSum = dfs(node.right, currentNumber);

        // Return the total sum
        return leftSum + rightSum;
    }

    // Start the DFS with the root and initial number 0
    return dfs(root, 0);
}

// Example usage:
let root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);

console.log(sumNumbers(root)); // Output: 25 (12 + 13)

root = new TreeNode(4);
root.left = new TreeNode(9);
root.right = new TreeNode(0);
root.left.left = new TreeNode(5);
root.left.right = new TreeNode(1);

console.log(sumNumbers(root)); // Output: 1026 (495 + 491 + 40)

4) Explanation of the solution in an easy-to-understand way. Explain it like a 10-year-old.

Imagine you have a tree, and each branch has numbers on it. You start at the root and move to the leaves, collecting numbers along the way to form a big number. When you reach a leaf, you add the big number to your total sum. You do this for all branches and then add up all the big numbers you collected.

5) Code explanation in pointers

  • Define a TreeNode class to represent each node in the tree.

  • Create a sumNumbers function that:

    • Defines a helper function dfs to:

      • Return 0 if the node is null (base case).

      • Update the current number by appending the node's value.

      • Return the current number if the node is a leaf.

      • Recursively calculate the sum for the left and right subtrees.

      • Return the total sum of the left and right subtrees.

    • Start the DFS with the root and initial number 0.

  • Use the sumNumbers function to calculate the total sum of all root-to-leaf numbers.

Note : When traversing a binary tree to form numbers from root to leaf, we need to concatenate the node values as digits to form a single number. For example, if we move from the root node with value 1 to a child node with value 2, the number formed should be 12.

6) Complexities

  • Time Complexity: (O(n)) - Each node is visited once.

  • Space Complexity: (O(h)) - Where (h) is the height of the tree. This is due to the recursion stack.

TreeTrees